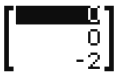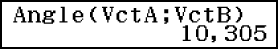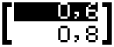Pro provedení 2-dimenzionálních a 3-dimenzionálních výpočtů vektorů použijte režim Vektor. Pro výpočet vektorů použijte speciální vektorové proměnné (VctA, VctB, VctC, VctD) (viz následující příklad).
|
Příklad: (1, 2) + (3, 4) |
|
|
1.Stiskněte 2.Stiskněte |
|
|
Zobrazí se vektorový editor pro vložení 2-rovinného vektoru pro VctA. |
|
|
3.Zadejte základní prvky VctA: 1 4.Proveďte tuto klávesovou operaci: 5.Zadejte základní prvky VctB: 3 6.Stisknutím |
|
|
Zobrazí se obrazovka VctAns (Paměť vektorových odpovědí) s výsledky výpočtu. |
|
Kdykoli je výsledkem prováděného výpočtu v režimu Vektor, obrazovka VctAns zobrazí výsledek. Výsledek bude také přiřazen k proměnné označené „VctAns“.
Proměnná VctAns může být použita ve výpočtech jak je popsáno níže.
Pro zadání proměnné VctAns do výpočtu proveďte následující klávesové operace: 
(VctAns).
Stisknutí jakékoli z následujících kláves, zatímco je zobrazena obrazovka VctAns, automaticky přepne na obrazovku výpočtů: 
, 
, 
, 
.
Přiřazení nových dat k vektorové proměnné
1.Stiskněte (Defin vektor) a potom v zobrazené nabídce vyberte vektorovou proměnnou, ke které chcete přiřadit data.
2.V zobrazeném dialogovém okně stisknutím 
nebo 
určete rovinu vektoru.
3.Pro vložení základních prvků vektoru použijte zobrazený vektorový editor.
Úpravy základních prvků vektorové proměnné
Stiskněte (Upravit vektor) a potom v zobrazené nabídce vyberte vektorovou proměnnou, kterou chcete upravit.
Kopírování obsahu vektorové proměnné (nebo VctAns)
1.Pro zobrazení vektoru, který chcete kopírovat, použijte vektorový editor.
Pokud chcete kopírovat obsah VctAns, proveďte následující pro zobrazení obrazovky VctAns: (VctAns)
.
2.Stiskněte 
a pak proveďte jednu z následujících klávesových operací pro určení místa určeného pro kopírování: 
(VctA), 
(VctB), 
(VctC) nebo 
(VctD).
Zobrazí se vektorový editor s obsahem místa určení pro kopírování.
V následujících příklade je použito VctA = (1, 2), VctB = (3, 4) a VctC = (2, -1, 2).
|
VctA • VctB (Skalární součin vektorů) |
|
|
|
|
|
VctA × VctB (Vektorový součin) |
|
|
|
|
|
Výpočet absolutních hodnot VctC (Abs(VctC)) |
|
|
|
|
|
Určení úhlu, který tvoří VctA a VctB (Angle(VctA;VctB)), na tři desetinná místa (Pev(Fix) 3). (Jednotka úhlu: Stupeň (D))
|
|
|
VctB |
|
|
Normalizace VctB (UnitV(VctB)) |
|
|
|
|
